Question 1: Part A:
You have been asked to design a cache with the following properties:
- Data words are 32 bits each
- A cache block will contain 2048 bits of data
- The cache is direct mapped
- The address supplied from the CPU is 32 bits long
- There are 2048 blocks in the cache
- Addresses are to the word
Pictured below is the general structure of a cache. There are 8 fields (labeled a, b, c, d, e, f, g, and h) . In the space below youʼll need to indicate the proper name or number of bits for a particular portion of this cache configuration. Whether a name or number should be entered will be specified:
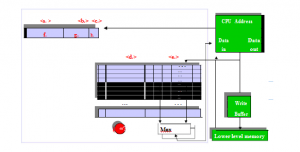
Suggestion – you donʼt have to fill in the answers “in order”. In fact, you need to determine the number of bits associated with the index and offset for example before determining the number of bits in the tag. Iʼll present the answer this way:
- (name)
– You are being asked to show what part of a physical address form the index, offset, and tag. < f > refers to the most significant bits of the address – so this is the tag.
- (name)
– It follows that the next part of the address is the index. h. (name)
– The least significant bits form the offset.
- (number)
- There are 211 bits / block and there are 25 bits / word. Thus there are 26 words / block so we need 6 bits of offset.
- (number)
- There are 211 blocks and the cache is direct mapped (or “1-way set associative”). Therefore, we need 11 bits of index.
- (number)
- The remaining bits form the tag. Thus, 32 – 6 – 11 à 15 bits of tag. (number)
- Field < d > refers to the fact that a tag must be stored in each block. Thus, 15 bits are kept in each block.
- (number)
- Field < e > asks you to specify the total number of bits / block. This is 2048.
- What 3 things must be compared at ? to determine if the cache entry is useable or not?
– We need to compare the valid bit associated with the block, the tag stored in the block, and the tag associated with the physical address. The tags should be the same and the valid bit should be 1.
- What is the total size of the cache?
– There are 2048 blocks in the cache and there are 2048 bits / block. o There are 8 bits / byte
o Thus, there are 256 bytes / block
– 2048 blocks x 256 bytes / block à 219 bytes (or 0.5 MB)
Part B:
Now, letʼs consider what happens if we make our cache 2-way set-associative instead of direct mapped. However, as before, the following still applies:
- Data words are 32 bits each
- A cache block will contain 2048 bits of data
- The address supplied from the CPU is 32 bits long
- There are 2048 blocks in the cache
- Addresses are to the word
Number of bits in offset?
- There are still 6 bits in the offset; data is still word addressed
Number of bits in index?
– We now need one less bit of index because we address to the set o 211 blocks / 21 blocks/set = 210 sets
o (10 bits of index needed)
Number of bits in tag?
- 32 – 6 – 10 = 16 bits.
Part C:
Now, letʼs consider what happens if we make our cache 4-way set-associative instead of direct mapped. However, as before, the following still applies:
- Data words are 32 bits each
- A cache block will contain 2048 bits of data
- The address supplied from the CPU is 32 bits long
- There are 2048 blocks in the cache
- Addresses are to the word
Number of bits in offset?
- There are still 6 bits in the offset; data is still word addressed
Number of bits in index?
– We now need one less bit of index because we address to the set o 211 blocks / 22 blocks/set = 29 sets
o (9 bits of index needed)
Number of bits in tag?
- 32 – 6 – 9 = 17 bits.
Part D:
Now, letʼs consider what happens if data is byte addressable. Weʼll keep the cache 4-way set associative for this question. However, as before, the following still applies:
- Data words are 32 bits each
- A cache block will contain 2048 bits of data
- The address supplied from the CPU is 32 bits long
- There are 2048 blocks in the cache
Number of bits in offset?
- There were 6 bits in the offset
- Now, each of the 4 bytes of a given word can be individually addressed o Therefore, we need 2 more bits of address per word
- Thus, 26 words * 22 bytes / word à 28
o 8 bits of offset are needed.
Number of bits in index?
– We need the same number of index bits as in Part D o 211 blocks / 22 blocks/set = 29 sets
o (9 bits of index needed)
Number of bits in tag?
- 32 – 8 – 9 = 15 bits.
Part E:
Now, letʼs consider what happens if the size of our physical address changes from 32 bits to 64 bits. Weʼll keep the cache 4- way set associative and data will still be addressable to the byte for this question. However, as before, the following still applies:
- A cache block will contain 2048 bits of data
- There are 2048 blocks in the cache
Number of bits in offset?
- 8 (as above)
Number of bits in index?
- 9 (as above)
Number of bits in offset?
- 64 – 8 – 9 = 47 bits
Question 2:
Our system has a main memory with 16 megabytes of addressable locations and a 32 kilobyte direct mapped cache with 8 bytes per block. The minimum addressable unit is a byte.
Part A:
How many blocks are there in the cache?
- (1 block / 23 bytes) x (215 bytes / cache) = 212 blocks / cache
- Therefore, need 12 bits of index
Part B:
Show how the main memory address is partitioned.
- 16 MB of addressable locations implies 24 bits of address are needed (224 = 16 MB)
- Therefore, need:
o 3 bits of offset o 12 bits of index o 9 bits of tag
Question 3:
Find the average memory access time for a processor given the following:
- The clock rate is 1 ns
- The miss penalty is 25 clock cycles
- 1% of instructions are not found in the cache.
- 5% of data references are not found in the cache
- 15% of memory accesses are for data.
- The memory system has a cache access time (including hit detection) of 1 clock cycle.
- Assume that the read and write miss penalties are the same and ignore other write stalls.
| AMAT | = | Hit Time | + | Miss Rate | x | Miss Penalty |
| = | 1 ns | + | (0.01 x 0.85 + 0.05 x 0.15) | x | 25 ns | |
| = | 1 ns | + | 0.16 | x | 25 ns | |
| = | 1.4 ns |
Question 4:
Consider a cache with the following specs:
- It is 4-way set associative
- It holds 64 Kbytes of data
- Data words are 32 bits each
- Data words are not byte addressed, they are word addressed
- A physical address is 40 bits.
- There are 16 words per cache block
- A First in, First out replacement policy is used for each set
- All cache entries are initially empty (i.e. their valid bits are not set)
At startup, the following physical addresses (in hexidecimal) are supplied to this cache in the order shown below:
| MSB | LSB | |||||||||
| 1 | F | F | F | B | D | 0 | 9 | 8 | 7 | 3 |
| 2 | A | B | C | D | E | F | 1 | 1 | 8 | 3 |
| 3 | A | B | C | D | E | F | 2 | 1 | 8 | 3 |
| 4 | A | B | C | D | E | F | 1 | 1 | 8 | 4 |
| 5 | A | B | C | D | E | F | 1 | 1 | 8 | 4 |
| 6 | F | F | F | B | D | 0 | 9 | 8 | 7 | 4 |
| 7 | F | F | F | B | D | 0 | A | 9 | 7 | 4 |
| 8 | F | F | F | B | D | 0 | A | 8 | 7 | 8 |
| 9 | A | B | C | D | E | F | 2 | 1 | 8 | 3 |
- There are 16 (2^4) addressable entries / block
- Thus, we need 4 bits of offset
- How many bits of index are needed?
- =216 bytes x (1 word / 22 bytes) x (1 block / 24 words) x (1 set / 22 blocks)
o = 28 sets
- Therefore, need 8 bits of index.
- The remaining (40 – 4 – 8 = 28) 28 bits form the tag
| Reference | Set reference | Status | Comment |
| maps to: | |||
| 1 | 87 | Compulsory Miss | 1st access |
| 2 | 18 | Compulsory Miss | 1st access |
| 3 | 18 | Compulsory Miss | 1st access; tag different than reference 2 |
| 4 | 18 | Hit | Data brought in during reference 2 |
| 5 | 18 | Hit | Data brought in during reference 2 |
| 6 | 87 | Hit | Data brought in during reference 1 |
| 7 | 97 | Compulsory Miss | Nothing else has mapped to set 97 |
| 8 | 87 | Compulsory Miss | Tag same as reference 7, but maps to |
| different set | |||
| 9 | 18 | Hit | Data brought in during reference 3 |