BINARY TREE AND ITS PROPERTIES PROOF

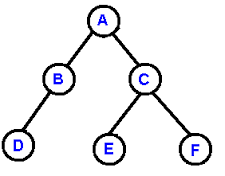This entry was posted in DATA STRUCTURE and tagged BINARY TREE on by

BINARY TREE

An important category of general tree is Binary Tree. A  binary tree can be defined as a finite collection of nodes where each node is having the property that it can have 0,1 or 2 children.
 
A binary tree may be empty known as Null tree or it contains a special node called the root of the tree and remaining nodes in the tree form the left and right binary sub-trees.


binary                                                     fig. (a) A binary tree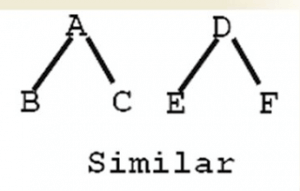

Here, the node A is the root of the binary tree which is the top of the tree.
 
B and C are the left and right sub-trees of the root A, respectively.
 
The left sub-tree namely B, having single node D.
 
The right sub-tree namely C having two nodes E and F.
 
 
 
Similar Binary tree
 
Two trees are called similar if both are having same structure but the elements in both the tree can be different as shown in fig. b
 
 
similar bt

                                                fig. b similar binary tree



Equivalent Binary tree

Two trees are called equivalent if both are having same structure and having the same content in their respective nodes.
 
 
Complete binary Tree 
 
A binary tree is called complete if it contains the maximum number of nodes it can have as shown in fig. c
 
 
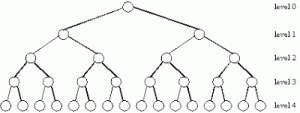
complete bt
                                                          fig. c   complete binary tree
 
 
 
On the other hand, a binary tree is said to be almost complete binary tree if all its levels are full except the last one as shown in fig. d
 
    almost                                                             
                                        fig. d almost complete binary tree

 In fig. c , at level k, there can be maximum 2^k nodes. therefore,
 level 0 can have 2^0=1 node.
 level 1 can have 2^1=2 nodes. 
 level 2 can have 2^2=4 nodes and so on.

Strictly Binary tree

A binary is called Strictly binary tree if all the non leaf nodes of the tree contains exactly two children.
It means , every non-leaf nodes contains left and right sub-tree.
It is also known as 2- tree or full Binary tree or extended binary tree.
It contains exactly 2n-1 nodes.

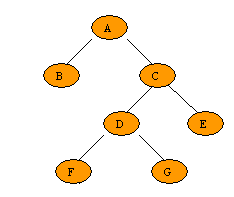
                                                                strictly bt


fig.e  strictly binary tree

 

BINARY TREE PROPERTIES:

  1. A Binary tree with n nodes has exactly n-1 edges.
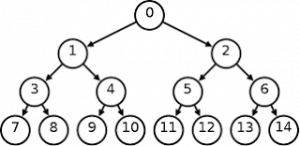
   index

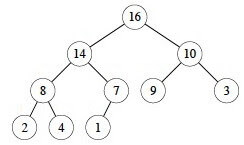
                                                           fig.1  binary tree

In the above fig. 1, number of nodes(n) are 15
number of edges= n-1=15-1=14

2. Every node except the root node has exactly one parent.
In the above fig. 1, A is the root node having no parent but rest nodes having only one parent i.e 3 has parent 1, 5 has parent 2.

3.There is exactly one path connecting any two nodes in the tree.
In the above fig. 1, you can see there is only one path between 0 to 1 or 1 to 3.

4. The maximum number of nodes at level ‘l’ of a binary tree is 2l-1
In the above fig. 1, level 1 has only one node 2^(1-1)=2^0=1
level 2 has 2  nodes 2^(2-1)=2^1=2 and so on.

5. Maximum number of nodes in a binary tree of height ‘h’ is 2h – 1.
In the above fig. 1, height of binary tree is 4(starting from 1 ,2,3,4)
Apply formula, Total number of nodes in a binary tree is 2^(4)-1=15

6. The number of leaf nodes in a complete binary tree is (n+1)/2
In the above fig. 1, number of nodes is 15
number of leaf nodes= (15+1)/2= 8 i.e node 7 to 14.

7. In a complete binary tree, number of external nodes= number of internal + 1
In the above fig. 1, number of internal nodes are 7 i.e 0 to 6
number of external nodes are 8 i.e 7 to 14

Leave a comment