GRAPHS IN COMPUTER SCIENCE AND ITS TYPES

This entry was posted in DATA STRUCTURE DISCRETE MATHEMATICS and tagged TYPES OF GRAPHS on by

Graph- Introduction

A Graph is a data structure consisting of vertices and edges. the theory associated with graph is called graph theory.

It can be used to solve many problems such as Planning routes for goods or services delivery, finding the shortest path, finding number of colours needed to colour the regions of a map and so on.

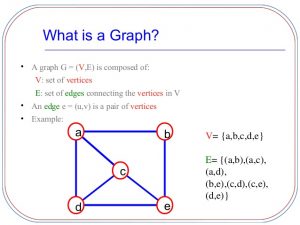
Graph is a data structure that consists of following two components:
1. A finite set of vertices also called as nodes.
2. A finite set of ordered pair of the form (u, v) called as edge. The pair is ordered because (u, v) is not same as (v, u) in case of directed graph(di-graph). The pair of form (u, v) indicates that there is an edge from vertex u to vertex v. The edges may contain weight/value/cost.

graphs-in-data-structure

 

Types of graph:

  1. Connected graph
  2. Directed graph
  3. Tree graph
  4. Weighted graph
  5. Acyclic graph and cyclic graph
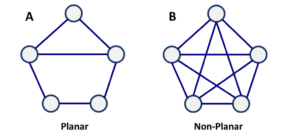
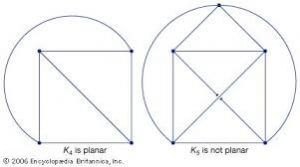
  6. Planner graph and non-planner  graph
  7. Multigraph graph
  8. Pseudograph graph
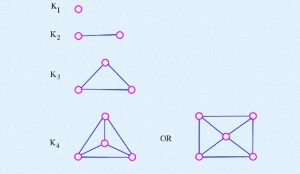
  9. Complete graph
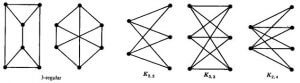
  10. Bipartite graph
  11. Regular Graph
  12. Cube Graph and Peterson Graph
  13. Path Graphs and NULL garph
  14. Isomorphic Graphs, walk and trail-path

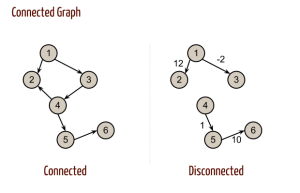
Connected Graph:

A graph is said to be connected if there is a path between connecting every pair of nodes or vertices.

A graph which is not connected can be divided into connected components call disjoint connected subgraphs.

1

 

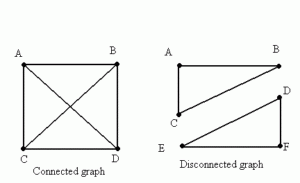
Disconnected graph

Graphs can be connected and disconnected. This means that the graph is constructed out of two or more sub-graphs without a path between these components. You can think of a disconnected graph as for the roads of the UK and France, since they aren’t connected by land.

 

Another Example:

A graph G is connected if there is a path in G between any given pair of vertices, otherwise it is disconnected. Every disconnected graph can be split up into a number of connected subgraphs, called components.

2

 

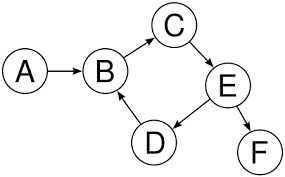
Directed Graph:

A directed graph or diagraph is a graph in which all the edges are directed. 

In a directed graph, we represent an edge from i to j as pair(i,j).  The formal description of a directed graph G is (V,E) where V is the set of vertices and E is the set of edges.

 A directed graph is shown in the following figure:

1

 

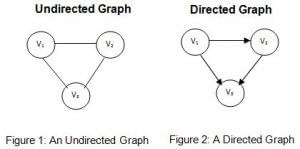
Undirected graph

As clear to its name,It is collection of vertices and edges that are connected together without any direction.

2

 

TREE INTRODUCTION

A graph is a called a tree if it is connected and contain no loop.

A tree may contain a special node called the root node of the tree. The exterior nodes of the tree are called leaves of the tree.

A graph with n  odes has exactly n-1 edges.

we can say that graph A is as subgraph of graph B if the nodes of A are a subset of the nodes of B and the edges of A are the edges of B on the corresponding nodes.

1

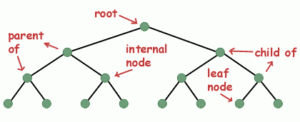
Properties of tree:

  1. A tree has exactly one root
  2. A tree has no cycle
  3. Vertices with same parent are called sibling
  4. Vertex without children is called leaf
  5. Vertices that have children are called internal vertices.
  6. Degree of a tree is the maximum allowed degree of any node in the tree.
  7. Depth of a vertex in a tree is the length of the unique path from the root of the tree to the vertex.
  8. A tree with n vertices has n-1 edges.
  9. In a tree there is one path between every pair of vertices
  10. if a connected graph with n vertices has n-1 edges then it is tree.
  11. If a graph with no loops has n vertices and n-1 edges then it is tree.

 

Weighted Graph

A graph is said to be weighted graph if some real number is assigned on every edge of a graph. 

the weight may be some value, any variable and so on.

1

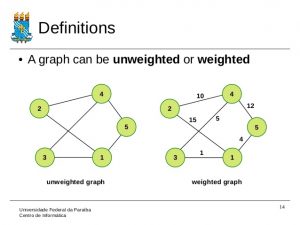
UnWeighted Graph

An unweighted directed graph (ugraph) is represented as a list of (vertex-neighbours) pairs, where the pairs are in standard order (as produced by key sort with unique keys) and the neighbours of each vertex are also in standard order (as produced by sort), every neighbour appears as a vertex even if it has no neighbours itself, and no vertex is a neighbour to itself.

 

Planar and Non-Planar Graphs
Graph A is planar since no link is overlapping with another. Graph B is non-planar since many links are overlapping. Also, the links of graph B cannot be reconfigured in a manner that would make it planar.
1
k4 is a planner and k5 is non – planner
2

Pseudograph

A pseudograph is a non-simple graph in which both graph loops and multiple edges are permitted.
Complete Graph
A computer graph is a graph in which every two distinct vertices are joined by exactly one edge. The complete graph with n vertices is denoted by  Kn.The following are the examples of complete graphs.
com-768x446
Bipartite graph
A bipartite graph, also called a bigraph, is a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacentExamples:

bi

 

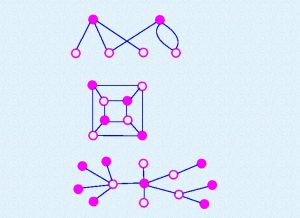
Regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbours; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other.

reg

 

Leave a comment