Following questions have been asked in GATE 

1) An undirected graph G(V, E) contains n ( n > 2 ) nodes named v1 , v2 ,….vn. Two nodes vi , vj are connected if and only if 0 < |i – j| <= 2. Each edge (vi, vj ) is assigned a weight i + j. A sample graph with n = 4 is shown below.

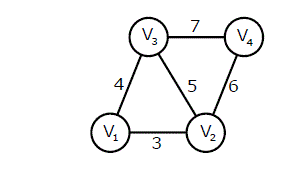
What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes?
(A) 1/12(11n^2 – 5n)
(B) n^2 – n + 1
(C) 6n – 11
(D) 2n + 1

Answer: (B)
Minimum spanning tree for 2 nodes would be

 (v1) _ (v2) 

Total weight 3

Minimum spanning tree for 3 nodes would be

 (v1) _ (v2) 
    |
 (v3)

Total weight= 3 + 4 = 7

Minimum spanning tree for 4 nodes would be

 (v1) _ (v2) _ (v4) 
    |
 (v3)

Total weight= 3 + 4 + 6 = 13

Minimum spanning tree for 5 nodes would be

 (v1) _ (v2) _ (v4) 
    |
 (v3)
    |
 (v5)

Total weight= 3 + 4 + 6 + 8 = 21

Minimum spanning tree for 6 nodes would be

 (v1) _ (v2) _ (v4) _ (v6)
    |
 (v3)
    |
 (v5)

Total weight= 3 + 4 + 6 + 8 + 10 = 31

We can observe from above examples that when we add kth node, the weight of spanning tree increases by 2k-2. Let T(n) be the weight of minimum spanning tree. T(n) can be written as

T(n) = T(n-1) + (2n-2) for n > 2
T(1) = 0, T(2) = 0 and T(2) = 3

The recurrence can be written as sum of series (2n – 2) + (2n-4) + (2n-6) + (2n-8) + …. 3 and solution of this recurrence is n^2 – n + 1.

2) The length of the path from v5 to v6 in the MST of previous question with n = 10 is
(A) 11
(B) 25
(C) 31
(D) 41

Answer: (C)
Any MST which has more than 5 nodes will have the same distance between v5 and v6 as the basic structure of all MSTs (with more than 5 nodes) would be following.

 (v1) _ (v2) _ (v4) _  (v6) _ .  . (more even numbered nodes)
    |
 (v3)
    |
 (v5)
    |
    .
    .
(more odd numbered nodes)

Distance between v5 and v6 = 3 + 4 + 6 + 8 + 10 = 31

3) Consider two binary operators ‘↑ ‘ and ‘↓’ with the precedence of operator ↓ being lower than that of the ↑ operator. Operator ↑ is right associative while operator ↓ is left associative. Which one of the following represents the parse tree for expression (7 ↓ 3 ­↑ 4 ­↑ 3 ↓ 2)?

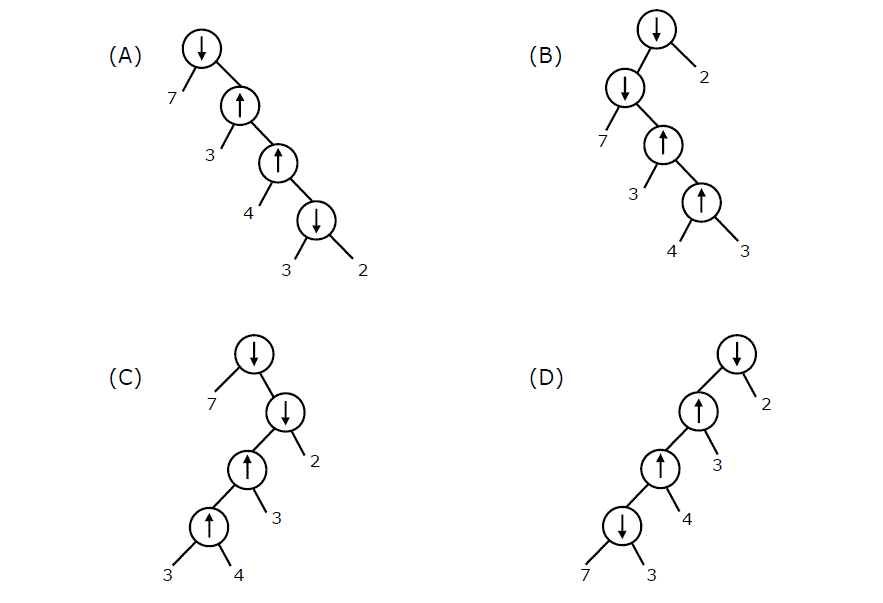
Answer: (B)
Let us consider the given expression (7 ↓ 3 ↑ 4 ↑ 3 ↓ 2).

Since the precedence of ↑ is higher, the sub-expression ([3 ↑ 4 ↑ 3) will be evaluated first. In this sub-expression, 4 ↑ 3 would be evaluated first because ↑ is right to left associative. So the expression is evaluated as ((7 ↓ (3 ↑ (4 ↑ 3))) ↓ 2). Also, note that among the two ↓ operators, first one is evaluated before the second one because the associativity of ↓ is left to right.

4) A max-heap is a heap where the value of each parent is greater than or equal to the values of its children. Which of the following is a max-heap?

Answer: (B)
A binary tree is max-heap if it is a complete binary tree (A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible) and it follows the max-heap property (value of each parent is greater than or equal to the values of its children).

A) is not a max-heap because it is not a complete binary tree
B) is a max-heap because it is complete binary tree and follows max-heap property.
C) is not a max-heap because 8 is a chile of 5 in this tree, so violates the max-heap property.
D) is not a max-heap because 8 is a chile of 5 in this tree, so violates the max-heap property. There are many other nodes in this tree which violate max-heap property in this tree.

5) Four matrices M1, M2, M3 and M4 of dimensions pxq, qxr, rxs and sxt respectively can be multiplied is several ways with different number of total scalar multiplications. For example, when multiplied as ((M1 X M2) X (M3 X M4)), the total number of multiplications is pqr + rst + prt. When multiplied as (((M1 X M2) X M3) X M4), the total number of scalar multiplications is pqr + prs + pst.

If p = 10, q = 100, r = 20, s = 5 and t = 80, then the number of scalar multiplications needed is
A) 248000
B) 44000
C) 19000
D) 25000

Answer (C)
We get minimum number of multiplications using ((M1 X (M2 X M3)) X M4).

Total number of multiplications = 100x20x5 (for M2 x M3) + 10x100x5 + 10x5x80 = 19000.

6) Which of the given options provides the increasing order of asymptotic complexity of functions f1, f2, f3 and f4?

f1(n) = 2^n
f2(n) = n^(3/2)
f3(n) = nLogn
f4(n) = n^(Logn)

A) f3, f2, f4, f1
B) f3, f2, f1, f4
C) f2, f3, f1, f4
D) f2, f3, f4, f1

Answer (A)

8) We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with the given set so that it becomes a binary search tree?
A) 0
B) 1
C) n!
D) (1/(n+1)).2nCn

Answer (B)

9) An algorithm to find the length of the longest monotonically increasing sequence of numbers in an array A[0 :n-1] is given below.
Let Li denote the length of the longest monotonically increasing sequence starting at index i in the array

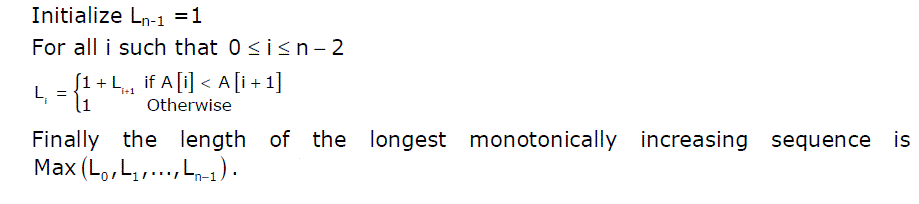
Which of the following statements is TRUE?
(A) The algorithm uses dynamic programming paradigm
(B) The algorithm has a linear complexity and uses branch and bound paradigm
(C) The algorithm has a non-linear polynomial complexity and uses branch and bound paradigm
(D) The algorithm uses divide and conquer paradigm.

Answer: (A)

10) Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}. Entry Wij in the matrix W below is the weight of the edge {i, j}.

What is the minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T?
(A) 7
(B) 8
(C) 9
(D) 10

Answer (D)

To get the minimum spanning tree with vertex 0 as leaf, first remove 0th row and 0th column and then get the minimum spanning tree (MST) of the remaining graph. Once we have MST of the remaining graph, connect the MST to vertex 0 with the edge with minimum weight (we have two options as there are two 1s in 0th row).

11. In the graph given in question 1, what is the minimum possible weight of a path P from vertex 1 to vertex 2 in this graph such that P contains at most 3 edges?
(A) 7
(B) 8
(C) 9
(D) 10

Answer (B)
Path: 1 -> 0 -> 4 -> 2
Weight: 1 + 4 + 3

12. The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1

(A) I and II
(B) III and IV
(C) IV only
(D) II and IV

Answer (D)

In sequence IV, we have a vertex with degree 8 which is not possible in a simple graph (no self loops and no multiple edges) with total vertex count as 8. Maximum possible degree in such a graph is 7.

In sequence II, four vertices are connected to 6 other vertices, but remaining 4 vertices have degrees as 3, 3, 2 and 2 which are not possible in a simple graph (no self loops and no multiple edges).

13. Consider a B+-tree in which the maximum number of keys in a node is 5. What is the minimum number of keys in any non-root node?
(A) 1
(B) 2
(C) 3
(D) 4

Answer (B)
Since the maximum number of keys is 5, maximum number of children a node can have is 6. By definition of B Tree, minimum children that a node can have would be 6/2 = 3. Therefore, minimum number of keys that a node can have becomes 2 (3-1).

14. The following C function takes a simply-linked list as input argument. It modifies the list by moving the last element to the front of the list and returns the modified list. Some part of the code is left blank.

Choose the correct alternative to replace the blank line.
(A) q = NULL; p->next = head; head = p;
(B) q->next = NULL; head = p; p->next = head;
(C) head = p; p->next = q; q->next = NULL;
(D) q->next = NULL; p->next = head; head = p;

Answer(D)
When the while loop ends, q contains address of second last node and p contains address of last node. So we need to do following things after while loop.
i) Set next of q as NULL (q->next = NULL).
ii) Set next of p as head (p->next = head).
iii) Make head as p ( head = p)
Step (ii) must be performed before step (iii). If we change head first, then we lose track of head node in the original linked list.

15. A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below.

Which one of the following choices gives a possible order in which the key values could have been inserted in the table?
(A) 46, 42, 34, 52, 23, 33
(B) 34, 42, 23, 52, 33, 46
(C) 46, 34, 42, 23, 52, 33
(D) 42, 46, 33, 23, 34, 52

Answer (C)
The sequence (A) doesn’t create the hash table as the element 52 appears before 23 in this sequence.
The sequence (B) doesn’t create the hash table as the element 33 appears before 46 in this sequence.
The sequence (C) creates the hash table as 42, 23 and 34 appear before 52 and 33, and 46 appears before 33.
The sequence (D) doesn’t create the hash table as the element 33 appears before 23 in this sequence.

16. How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?
(A) 10
(B) 20
(C) 30
(D) 40

Answer (C)
In a valid insertion sequence, the elements 42, 23 and 34 must appear before 52 and 33, and 46 must appear before 33.
Total number of different sequences = 3! x 5 = 30
In the above expression, 3! is for elements 42, 23 and 34 as they can appear in any order, and 5 is for element 46 as it can appear at 5 different places.

17. Which one of the following is a key factor for preferring B-trees to binary search trees for indexing database relations?
(a) Database relations have a large number of records
(b) Database relations are sorted on the primary key
(c) B-trees require less memory than binary search trees
(d) Data transfer form disks is in blocks.

Answer (d)
A disk block contains fairly large number of keys. Unlike BST where each node contains only one key, B-Tree is designed to contain large number of keys so that tree height is small.

18. How many distinct binary search trees can be created out of 4 distinct keys?
(a) 5
(b) 14
(c) 24
(d) 42

Answer (b)

Here is a systematic way to enumerate these BSTs. Consider all possible binary search trees with each element at the root. If there are n nodes, then for each choice of root node, there are n – 1 non-root nodes and these non-root nodes must be partitioned into those that are less than a chosen root and those that are greater than the chosen root.

Let’s say node i is chosen to be the root. Then there are i – 1 nodes smaller than i and n – i nodes bigger than i. For each of these two sets of nodes, there is a certain number of possible subtrees.

Let t(n) be the total number of BSTs with n nodes. The total number of BSTs with i at the root is t(i – 1) t(n – i). The two terms are multiplied together because the arrangements in the left and right subtrees are independent. That is, for each arrangement in the left tree and for each arrangement in the right tree, you get one BST with i at the root.

Summing over i gives the total number of binary search trees with n nodes.

The base case is t(0) = 1 and t(1) = 1, i.e. there is one empty BST and there is one BST with one node.

19. In a complete k-ary tree, every internal node has exactly k children. The number of leaves in such a tree with n internal nodes is:
(a) nk
(b) (n – 1) k+ 1
(c) n( k – 1) + 1
(d) n(k – 1)

Answer (c)

20) Suppose T(n) = 2T(n/2) + n, T(0) = T(1) = 1
Which one of the following is false.
a) T(n) = O(n^2)
b) T(n) = Θ(nLogn)
c) T(n) = Ω(n²)
d) T(n) = O(nLogn)

Answer (c)
The given recurrence relation can be solved using Master Theorem. It lies in case 2 of Master Theorem. Or, if you remember recurrence relation of Merge Sort or best case Quick Sort, you can guess the value of T(n).

T(n) = Θ(nLogn)

By definition of Big O notation, we can say.
Θ(nLogn) = O(nLogn) = O(n^2)

Θ(nLogn) ca be equal to Ω(n) or Ω(nLogn), but not Ω(n^2)