1. Let S be an NP-complete problem and Q and R be two other problems not known to be in NP. Q is polynomial time reducible to S and S is polynomial-time reducible to R. Which one of the following statements is true?
(A) R is NP-complete
(B) R is NP-hard
(C) Q is NP-complete
(D) Q is NP-hard
Answer (B)
(A) Incorrect because R is not in NP. A NP Complete problem has to be in both NP and NP-hard.
(B) Correct because a NP Complete problem S is polynomial time educable to R.
(C) Incorrect because Q is not in NP.
(D) Incorrect because there is no NP-complete problem that is polynomial time Turing-reducible to Q.
2) A set X can be represented by an array x[n] as follows:
Consider the following algorithm in which x,y and z are Boolean arrays of size n:
algorithm zzz(x[] , y[] , z[])
{
int i;
for ( i=0; i<n ; ++i)
z[i] = (x[i] ^ `y[i] V ( `x[i] ^y[i])
}
The set Z computed by the algorithm is:
(A) (X Intersection Y)
(B) (X Union Y)
(C) (X-Y) Intersection (Y-X)
(D) (X-Y) Union (Y-X)
Answer (D)
The expression x[i] ^ ~y[i]) results the only 1s in x where corresponding entry in y is 0. An array with these set bits represents set X – Y
The expression ~x[i] ^ y[i]) results the only 1s in y where corresponding entry in x is 0. An array with these set bits represents set Y – X.
The operator “V” results in Union of the above two sets.
3. Consider the following recurrence:
Which one of the following is true?
(A) T(n) = Θ(loglogn)
(B) T(n) = Θ(logn)
(C) T(n) = Θ(sqrt(n))
(D) T(n) = Θ(n)
Answer (B)
Let n = 2^m
T(2^m) = T(2^(m/2)) + 1
Let T(2^m) = S(m)
S(m) = 2S(m/2) + 1
Above expression is a binary tree traversal recursion whose time complexity is Θ(m). You can also prove using Master theorem.
S(m) = Θ(m)
= Θ(logn) /* Since n = 2^m */
Now, let us go back to the original recursive function T(n)
T(n) = T(2^m) = S(m)
= Θ(Logn)
Please note that the solution of T(n) = T(√n) + 1 is Θ(Log Log n), above recurrence is different, it is T(n) = 2T(√n) + 1
4. Let X be a problem that belongs to the class NP. Then which one of the following is TRUE?
(A) There is no polynomial time algorithm for X.
(B) If X can be solved deterministically in polynomial time, then P = NP.
(C) If X is NP-hard, then it is NP-complete.
(D) X may be undecidable.
Answer (C)
(A) is incorrect because set NP includes both P(Polynomial time solvable) and NP-Complete .
(B) is incorrect because X may belong to P (same reason as (A))
(C) is correct because NP-Complete set is intersection of NP and NP-Hard sets.
(D) is incorrect because all NP problems are decidable in finite set of operations.
5. What is the number of swaps required to sort n elements using selection sort, in the worst case?
(A) Θ(n)
(B) Θ(n log n)
(C) Θ(n2 )
(D) Θ(nn2 log n)
Answer (A)
Here is Selection Sort algorithm for sorting in ascending order.
1. Find the minimum value in the list
2. Swap it with the value in the first position
3. Repeat the steps above for the remainder of the list (starting at
the second position and advancing each time)
As we can see from the algorithm, selection sort performs swap only after finding the appropriate position of the current picked element. So there are O(n) swaps performed in selection sort.
Because swaps require writing to the array, selection sort is preferable if writing to memory is significantly more expensive than reading. This is generally the case if the items are huge but the keys are small. Another example where writing times are crucial is an array stored in EEPROM or Flash. There is no other algorithm with less data movement.
6. The running time of an algorithm is represented by the following recurrence relation:
if n <= 3 then T(n) = n
else T(n) = T(n/3) + cn
Which one of the following represents the time complexity of the algorithm?
(A) Θ(n)
(B) Θ(n log n)
(C) Θ(n2)
(D) Θ(n2 log n)
Answer(A)
T(n) = cn + T(n/3)
= cn + cn/3 + T(n/9)
= cn + cn/3 + cn/9 + T(n/27)
Taking the sum of infinite GP series. The value of T(n) will
be less than this sum.
T(n) <= cn(1/(1-1/3))
<= 3cn/2
or we can say
cn <= T(n) <= 3cn/2
Therefore T(n) = Θ(n)
This can also be solved using Master Theorem for solving recurrences. The given expression lies in Case 3 of the theorem.
4. The keys 12, 18, 13, 2, 3, 23, 5 and 15 are inserted into an initially empty hash table of length 10 using open addressing with hash function h(k) = k mod 10 and linear probing. What is the resultant hash table?
Answer (C)
Open addressing, or closed hashing, is a method of collision resolution in hash tables. With this method a hash collision is resolved by probing, or searching through alternate locations in the array (the probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. Well known probe sequences include:
linear probing in which the interval between probes is fixed–often at 1.
quadratic probing in which the interval between probes increases linearly (hence, the indices are described by a quadratic function).
double hashing in which the interval between probes is fixed for each record but is computed by another hash function.
8. Consider the polynomial p(x) = a0 + a1x + a2x^2 +a3x^3, where ai != 0, for all i. The minimum number of multiplications needed to evaluate p on an input x is:
(A) 3
(B) 4
(C) 6
(D) 9
Answer (A)
Multiplications can be minimized using following order for evaluation of the given expression.
p(x) = a0 + x(a1 + x(a2 + a3x))
9. To implement Dijkstra’s shortest path algorithm on unweighted graphs so that it runs in linear time, the data structure to be used is:
(A) Queue
(B) Stack
(C) Heap
(D) B-Tree
Answer(A)
The shortest path in an un-weighted graph means the smallest number of edges that must be traversed in order to reach the destination in the graph. This is the same problem as solving the weighted version where all the weights happen to be 1. If we use Queue (FIFO) instead of Priority Queue (Min Heap), we get the shortest path in linear time O(|V| + |E|). Basically we do BFS traversal of the graph to get the shortest paths.
10. A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: The root is stored in the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to a[3]. The nodes from the second level of the tree from left to right are stored from a[4] location onward. An item x can be inserted into a 3-ary heap containing n items by placing x in the location a[n] and pushing it up the tree to satisfy the heap property.
Which one of the following is a valid sequence of elements in an array representing 3-ary max heap?
(A) 1, 3, 5, 6, 8, 9
(B) 9, 6, 3, 1, 8, 5
(C) 9, 3, 6, 8, 5, 1
(D) 9, 5, 6, 8, 3, 1
Answer (D)
9
/ | \
/ | \
5 6 8
/ |
/ |
3 1
11. Suppose the elements 7, 2, 10 and 4 are inserted, in that order, into the valid 3- ary max heap found in the above question, Which one of the following is the sequence of items in the array representing the resultant heap?
(A) 10, 7, 9, 8, 3, 1, 5, 2, 6, 4
(B) 10, 9, 8, 7, 6, 5, 4, 3, 2, 1
(C) 10, 9, 4, 5, 7, 6, 8, 2, 1, 3
(D) 10, 8, 6, 9, 7, 2, 3, 4, 1, 5
Answer(A)
After insertion of 7
9
/ | \
/ | \
7 6 8
/ | \
/ | \
3 1 5
After insertion of 2
9
/ | \
/ | \
7 6 8
/ | \ /
/ | \ /
3 1 5 2
After insertion of 10
10
/ | \
/ | \
7 9 8
/ | \ / |
/ | \ / |
3 1 5 2 6
After insertion of 4
10
/ | \
/ | \
7 9 8
/ | \ / | \
/ | \ / | \
3 1 5 2 6 4
12. Consider the following graph:
Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm?
(A) (a—b),(d—f),(b—f),(d—c),(d—e)
(B) (a—b),(d—f),(d—c),(b—f),(d—e)
(C) (d—f),(a—b),(d—c),(b—f),(d—e)
(D) (d—f),(a—b),(b—f),(d—e),(d—c)
Answer (D)
The edge (d-e) cannot be considered before (d-c) in Kruskal’s minimum spanning tree algorithm because Kruskal’s algorithm picks the edge with minimum weight from the current set of edges at each step.
13. The median of n elements can be found in O(n)time. Which one of the following is correct about the complexity of quick sort, in which median is selected as pivot?
(A) Θ(n)
(B) Θ(nlogn)
(C) Θ(n^2)
(D) Θ(n^3)
Answer (B)
If median is always used as pivot, then recursion remains T(n) = 2T(n/2) + cn for all the cases where cn is combined time for median finding and partition. So, worst case time complexity of this quick sort becomes Θ(nlogn). In practical implementations, however, this variant is considerably slower on average (seehttp://en.wikipedia.org/wiki/Quicksort#Selection-based_pivoting)
14. Consider a binary max-heap implemented using an array. Which one of the following array represents a binary max-heap?
(A) 25,12,16,13,10,8,14
(B) 25,14,13,16,10,8,12
(C) 25,14,16,13,10,8,12
(D) 25,14,12,13,10,8,16
Answer (C)
A tree is max-heap if data at every node in the tree is greater than or equal to it’s children’ s data.
In array representation of heap tree, a node at index i has its left child at index 2i + 1 and right child at index 2i + 2.
25
/ \
/ \
14 16
/ \ / \
/ \ / \
13 10 8 12
15. What is the content of the array after two delete operations on the correct answer to the previous question?
(A) 14,13,12,10,8
(B) 14,12,13,8,10
(C) 14,13,8,12,10
(D) 14,13,12,8,10
Answer(D)
For Heap trees, deletion of a node includes following two operations.
1) Replace the root with last element on the last level.
2) Starting from root, heapify the complete tree from top to bottom..
Let us delete the two nodes one by one:
1) Deletion of 25:
Replace 25 with 12
12
/ \
/ \
14 16
/ \ /
/ \ /
13 10 8
Since heap property is violated for root (16 is greater than 12), make 16 as root of the tree.
16
/ \
/ \
14 12
/ \ /
/ \ /
13 10 8
2) Deletion of 16:
Replace 16 with 8
8
/ \
/ \
14 12
/ \
/ \
13 10
Heapify from root to bottom.
14
/ \
/ \
8 12
/ \
/ \
13 10
14
/ \
/ \
13 12
/ \
/ \
8 10
16. In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?
(A) Θ(n)
(B) Θ(n Log n)
(C) Θ(n^2)
(D) Θ(n2 log n)
Answer(B)
The recursion expression becomes:
T(n) = T(n/4) + T(3n/4) + cn
After solving the above recursion, we get Θ(nLogn).
17. What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.
(A) 2
(B) 3
(C) 4
(D) 5
Answer(B)
AVL trees are binary trees with the following restrictions.
1) the height difference of the children is at most 1.
2) both children are AVL trees
a
/ \
/ \
b c
/ \ /
/ \ /
d e g
/
/
h
References:
http://en.wikipedia.org/wiki/AVL_tree
18. The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity.
(A) Θ(n)
(B) Θ(m)
(C) Θ(m + n)
(D) Θ(mn)
Answer (C)
Connected components can be found in O(m + n) using Tarjan’s algorithm. Once we have connected components, we can count them.
19. Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then
(A) T(n) <= 2T(n/5) + n
(B) T(n) <= T(n/5) + T(4n/5) + n
(C) T(n) <= 2T(4n/5) + n
(D) T(n) <= 2T(n/2) + n
Answer (B)
For the case where n/5 elements are in one subset, T(n/5) comparisons are needed for the first subset with n/5 elements, T(4n/5) is for the rest 4n/5 elements, and n is for finding the pivot. If there are more than n/5 elements in one set then other set will have less than 4n/5 elements and time complexity will be less than T(n/5) + T(4n/5) + n because recursion tree will be more balanced.
20 Dijkstra’s single source shortest path algorithm when run from vertex a in the below graph, computes the correct shortest path distance to
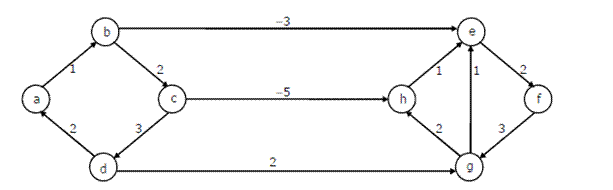
(A) only vertex a
(B) only vertices a, e, f, g, h
(C) only vertices a, b, c, d
(D) all the vertices
Answer (D)
Dijkstra’s single source shortest path is not guaranteed to work for graphs with negative weight edges, but it works for the given graph.
Let us see…
Let us run the 1st pass
b 1
b is minimum, so shortest distance to b is 1.
After 1st pass, distances are
c 3, e -2.
e is minimum, so shortest distance to e is -2
After 2nd pass, distances are
c 3, f 0.
f is minimum, so shortest distance to f is 0
After 3rd pass, distances are
c 3, g 3.
Both are same, let us take g. so shortest distance to g is 3.
After 4th pass, distances are
c 3, h 5
c is minimum, so shortest distance to c is 3
After 5th pass, distances are
h -2
h is minimum, so shortest distance to h is -2
21. The following C function takes a single-linked list of integers as a parameter and rearranges the elements of the list. The function is called with the list containing the integers 1, 2, 3, 4, 5, 6, 7 in the given order. What will be the contents of the list after the function completes execution?
struct node { int value; struct node *next;};void rearrange(struct node *list){ struct node *p, * q; int temp; if ((!list) || !list->next) return; p = list; q = list->next; while(q) { temp = p->value; p->value = q->value; q->value = temp; p = q->next; q = p?p->next:0; }} |
(A) 1,2,3,4,5,6,7
(B) 2,1,4,3,6,5,7
(C) 1,3,2,5,4,7,6
(D) 2,3,4,5,6,7,1
Answer (B)
The function rearrange() exchanges data of every node with its next node. It starts exchanging data from the first node itself.
21. The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
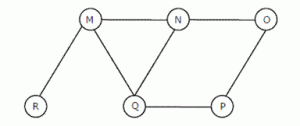
(A) MNOPQR
(B) NQMPOR
(C) QMNPRO
(D) QMNPOR
Answer (C)
22. Consider the following functions:
f(n) = 2^n g(n) = n! h(n) = n^logn
Which of the following statements about the asymptotic behaviour of f(n), g(n), and h(n) is true?
(A) f(n) = O(g(n)); g(n) = O(h(n))
(B) f(n) = Ω(g(n)); g(n) = O(h(n))
(C) g(n) = O(f(n)); h(n) = O(f(n))
(D) h(n) = O(f(n)); g(n) = Ω(f(n))
Answer (D)
According to order of growth: h(n) < f(n) < g(n) (g(n) is asymptotically greater than f(n) and f(n) is asymptotically greater than h(n) ) We can easily see above order by taking logs of the given 3 functions
lognlogn < n < log(n!) (logs of the given f(n), g(n) and h(n)).
Note that log(n!) = Θ(nlogn)
23. The minimum number of comparisons required to determine if an integer appears more than n/2 times in a sorted array of n integers is
(A) Θ(n)
(B) Θ(logn)
(C) Θ(log*n)
(D) Θ(n)
Answer (B)
24. The number of leaf nodes in a rooted tree of n nodes, with each node having 0 or 3 children is:
a) n/2
b) (n-1)/3
c) (n-1)/2
d) (2n+1)/3
Answer(d)
L = (3-1)I + 1 = 2I + 1
Total number of nodes(n) is sum of leaf nodes and internal nodes
n = L + I
After solving above two, we get L = (2n+1)/3
25. The running time of the following algorithm
Procedure A(n) If n <= 2 return(1) else return A();
is best described by
a) O(n)
b) O(log n)
c) O(1og log n)
d) O(1)
Answer(c)
26. A weight-balanced tree is a binary tree in which for each node. The number of nodes in the left sub tree is at least half and at most twice the number of nodes in the right sub tree. The maximum possible height (number of nodes on the path from the root to the farthest leaf) of such a tree on n nodes is best described by which of the following?
a) log2 n
b) log4/3 n
c) log3 n
d) log3/2 n
Answer(d)
Let the maximum possible height of a tree with n nodes is represented by H(n).
The maximum possible value of H(n) can be approximately written using following recursion
H(n) = H(2n/3) + 1
The solution of above recurrence is log3/2 n. We can simply get it by drawing a recursion tree.
27. Consider the following algorithm for searching for a given number x in an unsorted – array A[1..n] having n distinct values:
1) Choose an i uniformly at random from 1..n; 2) If A[i] = x then Stop else Goto 1;
Assuming that x is present in A, what is the expected number of comparisons made by the algorithm before it terminates?
a) n
b) n-l
c) 2n
d) n/2
Answer(a)
If you remember the coin and dice questions, you can just guess the answer for the above.
Below is proof for the answer.
Let expected number of comparisons be E. Value of E is sum of following expression for all the possible cases.
number_of_comparisons_for_a_case * probability_for_the_case
Case 1
If A[i] is found in the first attempt
number of comparisons = 1
probability of the case = 1/n
Case 2
If A[i] is found in the second attempt
number of comparisons = 2
probability of the case = (n-1)/n*1/n
Case 3
If A[i] is found in the third attempt
number of comparisons = 2
probability of the case = (n-1)/n*(n-1)/n*1/n
There are actually infinite such cases. So, we have following infinite series for E.
E = 1/n + [(n-1)/n]*[1/n]*2 + [(n-1)/n]*[(n-1)/n]*[1/n]*3 + …. (1)
After multiplying equation (1) with (n-1)/n, we get
E (n-1)/n = [(n-1)/n]*[1/n] + [(n-1)/n]*[(n-1)/n]*[1/n]*2 +
[(n-1)/n]*[(n-1)/n]*[(n-1)/n]*[1/n]*3 ……….(2)
Subtracting (2) from (1), we get
E/n = 1/n + (n-1)/n*1/n + (n-1)/n*(n-1)/n*1/n + …………
The expression on right side is a GP with infinite elements. Let us apply the sum formula (a/(1-r))
E/n = [1/n]/[1-(n-1)/n] = 1
E = n
28. Consider the process of inserting an element into a Max Heap, where the Max Heap is represented by an array. Suppose we perform a binary search on the path from the new leaf to the root to find the position for the newly inserted element, the number of comparisons performed is:
(A) Θ(logn)
(B) Θ(LogLogn )
(C) Θ(n)
(D) Θ(nLogn)
Answer (B)
The height of a Max Heap is Θ(logn). If we perform binary search for finding the correct position then we need to do Θ(LogLogn) comparisons.
29. Let w be the minimum weight among all edge weights in an undirected connected graph. Let e be a specific edge of weight w . Which of the following is FALSE?
(A) There is a minimum spanning tree containing e.
(B) If e is not in a minimum spanning tree T, then in the cycle formed by adding e to T, all edges have the same weight.
(C) Every minimum spanning tree has an edge of weight w .
(D) e is present in every minimum spanning tree.
Answer (D)
(A), (B) and (C) are correct.
(D) is incorrect as there may be many edges of wight w in the graph and e may not be picked up in some of the minimum spanning trees.
30. An array of n numbers is given, where n is an even number. The maximum as well as the minimum of these n numbers needs to be determined. Which of the following is TRUE about the number of comparisons needed?
(A) At least 2n – c comparisons, for some constant c, are needed.
(B) At most 1.5n – 2 comparisons are needed.
(C) At least nLog2n comparisons are needed.
(D) None of the above.
Answer (B)
31. Consider a hash table of size seven, with starting index zero, and a hash function (3x + 4)mod7. Assuming the hash table is initially empty, which of the following is the contents of the table when the sequence 1, 3, 8, 10 is inserted into the table using closed hashing? Note that ‘_’ denotes an empty location in the table.
(A) 8, _, _, _, _, _, 10
(B) 1, 8, 10, _, _, _, 3
(C) 1, _, _, _, _, _,3
(D) 1, 10, 8, _, _, _, 3
Answer (B)
Please see http://lcm.csa.iisc.ernet.in/dsa/node38.html for closed hashing and probing.
Let us put values 1, 3, 8, 10 in the hash of size 7.
Initially, hash table is empty
- - - - - - -
0 1 2 3 4 5 6
The value of function (3x + 4)mod 7 for 1 is 0, so let us put the value at 0
1 - - - - - -
0 1 2 3 4 5 6
The value of function (3x + 4)mod 7 for 3 is 6, so let us put the value at 6
1 - - - - - 3
0 1 2 3 4 5 6
The value of function (3x + 4)mod 7 for 8 is 0, but 0 is already occupied, let us put the value(8) at next available space(1)
1 8 - - - - 3
0 1 2 3 4 5 6
The value of function (3x + 4)mod 7 for 10 is 6, but 6 is already occupied, let us put the value(10) at next available space(2)
1 8 10 - - - 3
0 1 2 3 4 5 6
32. In an unweighted, undirected connected graph, the shortest path from a node S to every other node is computed most efficiently, in terms of time complexity by
(A) Dijkstra’s algorithm starting from S.
(B) Warshall’s algorithm
(C) Performing a DFS starting from S.
(D) Performing a BFS starting from S.
Answer(D)
* Time Comlexity of the Dijkstra’s algorithm is O(|V|^2 + E)
* Time Comlexity of the Warshall’s algorithm is O(|V|^3)
* DFS cannot be used for finding shortest paths
* BFS can be used for unweighted graphs. Time Complexity for BFS is O(|E| + |V|)
33. A complete n-ary tree is a tree in which each node has n children or no children. Let I be the number of internal nodes and L be the number of leaves in a complete n-ary tree. If L = 41, and I = 10, what is the value of n?
(A) 3
(B) 4
(C) 5
(D) 6
Answer (C)
For an n-ary tree where each node has n children or no children, following relation holds
L = (n-1)*I + 1
Where L is the number of leaf nodes and I is the number of internal nodes.
Let us find out the value of n for the given data.
L = 41 , I = 10
41 = 10*(n-1) + 1
(n-1) = 4
n = 5